Blog - Oyun/Yazılım geliştirmede istatistik ve olasılık

Ziyaretci:2643

Bir istatistik öğrencisi ve yazılım geliştirici olarak bazı istatistiksel kavramları daha elle tutulur hale getirmeye çalışıcam sebebi bazen öğrenilen şeyleri hayata katmak zorlaşıyor,o halde yazıya geçelim.

TANIMLAR

İlk olarak ne konuştuğumuzu bilmek adına hakkında konuşacağım başlıca kavramları tanımlayalım.

İstatistik:Rastsallık içeren olaylar,sistem ve süreçler hakkında modeller kurmak ve bu modellerden sonuç çıkarmada gerekli bilgileri sağlayan bir bilim dalıdır.

Olasılık :Matematikte, olasılık, bir olayın gerçekleşebilme ölçüsüdür.

Rassallık(rastgelelik):Bir olayın eşit olasılıklar ile dağıldığı gösteren kavram(kendim tanımladım)

Rassal Değişken:Gerçek hayattaki bir olayı ,matematiksel olarak açıklayabilmemiz için kullandığımız kavram.

Kesikli Rassal Değişken:0,1,2,3 gibi sayılabilen kümeye sahip yada sayılabilir sonsuz(rassal değişken) 0 den sonsuza kadar değer alabilir.

Sürekli Rassal Değişken: Alt ve üst sınıra sahip,Belirli bir alanda çalıştığımız sayılamayan /sayılamayan sonsuzluğa sahip değişkenlerdir.

Beklenen Değer(ortalama):Beklenen değer, olasılıkları kullanarak bize uzun vadede hangi sonuçları bekleyebileceğimizi söyleyen kavramdır.

Merkezi limit teoremi:büyük bir sayıda olan bağımsız ve aynı dağılıma sahip rassal değişkenlerin (eğer sonlu varyans değerleri bulunuyorsa)aritmetik ortalamasının yaklaşık olarak normal dağılım göstereceğini ifade eden teoremdir.

Kaos Kuramı:karmaşık/kaotik sistemleri sistemleri inceleyen, onlar hakkında anlamlı matematiksel sonuçlar çıkarmayı hedefleyen bir kuramdır.

GİRİŞ

Günlük hayatta geliştiriciler , istatistikçiler ve/veya matematikçiler|bilimle uğraşan insanlar birçok konuda olasılık kuramı ve istatik kullanarak sorunlarını çözüyor,kullanım alanlarına örnek olarak.

İstatistikçiler için : yapılan anket/çalışma/tahmin’in daha doğru ve tutarlı olması için en basitinden kan grubu tahmini,ilaç çalışmaları yapan bilim insanları(siyasi anketler örneğini kullanmayacağım)
Gelişticiler için :bir oyun yada bir özellikte kullanıcıya rastgele anda işlem yapmasını sağlamak .Örneğin :siz bir bilgisayar oyununda ilerlerken aniden karşınıza canavar veya düşman çıkması

(not:burada bahsedilen örneklerin uygulamalarını ve kaynak kodlarını yayınlayacağım)

TEORİK KISIM

Beklenen Değer

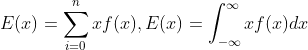
Yukarıda gördüğünüz seri ve integral formüllerini beklenen değer bulmak için kullanıyoruz.(Aslen yapılan iş aynı ikiside toplam işlemi yapıyor) fakat seri toplamı kesikli rassal değişkenlerde ,integral ise sürekli rassal değişkenlerde kullanılır .Not: bilgisayarda biz bu işi döngülerle yapıyoruz,toplamda integralde benzer yolla hesaplanır.

Merkezi Limit Teoremi

Her biri birbirinden bağımsız ve aynı dağılıma sahip rassal değişkenlerin , toplamı

Dağılımların ortalama tahmin edicisi ,Tahmin edicinin olasılığı ise seçilen bir rd beklenen değerine yakınsar.

seçilen yapılan dağılım ortalamasına eşit olur. Burada denklemleri düzgünce yazamadığım için destekleyici kaynak olarak bu uygulamanın kodları‘ini ekliyorum.Bu konuyla ilgili deney bu pdfte mevcuttur.

UYGULAMA / KOD

İşte sonunda beklenilen ,istenilen şeye geldik .Bunca teoremi formülü gerçek hayattaki birçok sorun için kullanacağız.

Uygulama-1(rassallık)

Bir geliştirici olduğunuzu düşünelim, patronunuz sizden indirim kuponlarını oluşturmak için bir uygulama(api) istedi.Öncelikli olarak kuponlarda istediğimiz her türlü ,harfi ,rakamı,sembolü kullanabiliyoruz .Her bir kupon benzersiz,kullandığımız ifadeleri rastgele olmalı eğer rastgele olmazsa müşterinin güvenini,dolayısı ile müşteri kaybedersiniz,neyse kodumuza geçelim. Not:Bu yazılımda çok fazla programlama hatası vardır.Konunun anlaşılması için basit bir örnek olarak sunulmuştur ! örnek servisin tamamı örnek servis

#gerekli kütüphaneler
import random
import string
#kuponların olduğu dizimiz
coupons=[]
#kupon oluşturduğumuz fonksiyon

def CouponCreator(number,length ):
  chars = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!@£$%^&*().,?0123456789'
  for cpn in range(number):
   coupon = ''
   print(coupons)
  for c in range(length):
   coupon += random.choice(chars)
   coupons.append(coupon)

#kaç adet kupon ve ne kadar büyüklükte olacağına karar veriyoruz
CouponCreator(2,2 )

#gerekli kütüphaneler

import random

import string

#kuponların olduğu dizimiz

coupons=[]

#kupon oluşturduğumuz fonksiyon

def CouponCreator(number,length ):

chars = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ!@£$%^&*().,?0123456789'

for cpn in range(number):

coupon = ''

print(coupons)

for c in range(length):

coupon += random.choice(chars)

coupons.append(coupon)

#kaç adet kupon ve ne kadar büyüklükte olacağına karar veriyoruz

CouponCreator(2,2 )

Hazırladığımız uygulumaya baktığımızda karakterleri rastgele (bunun rastgeleliliği tartışılır ) işlemler seçmemizi sağlayan “random.choice “fonksiyonunu inceleyelim.Eğer bu fonksiyon olmasa,karakterler arası rassal seçim yapmaya çalışan geliştiricinin işi oldukça zor olacak idi.Bilgisayarlardaki rastlantısallığı taklit etmek için kullanılan yalancı sayıların temeli kaos kuramından gelmektedir.

Uygulama-2

(beklenen değer)

Bu konuda şans oyunlarını ele alalım ,milli piyangoyu örnek verelim.1 ile 90 arası 6 sayı +1 joker sayı seçiyoruz ,her kolon için 3 tl ücret ödeyerek bilet parasını buluyoruz ardından her top bir defa çekilip iade edilmediği için olasılıkları teker teker azaltıyoruz.(1/90 * 1/89*1/88* 1/87*1/86*1/84*1/83) çekilişler birbirinden bağımsız gerçekleşiyor fakat

Bu şans oyunun eklenen değeri şu şekilde bulmalıyız: (7 topun gelme şansı)*bilet parası*büyük ikramiye

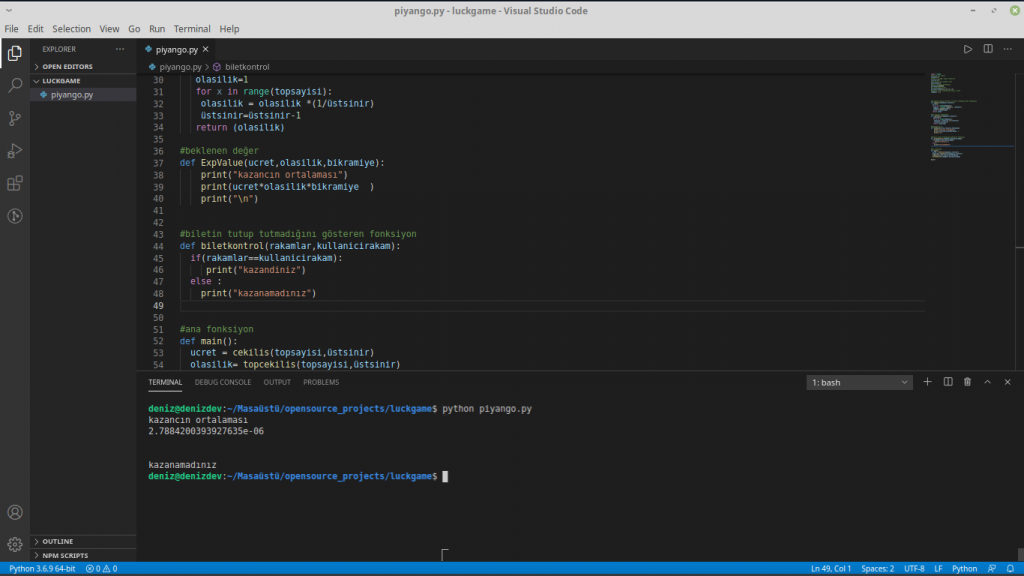
uygulamamızı çalıştırıp inceleyelim ardından ne yapmalıyız ona bakalım. kaynak kodu :piyango

import random
#cekilen top sayisi
topsayisi=7
#1 den n e kadar sayı üstsinir=n
üstsinir=90
#her kolon icin alınan ücret
kolonfiyati=3
#büyük ikramiye miktarları
bikramiye=5000000
#kullanıcının bileti
kullanicirakam=[1,2,3,4,1,2,2]
#kazanan bilet numaraların olduğu liste
rakamlar = []


#piyangoyu kazanan biletin ve bilet fiyatını bulan fonksiyonu 
def cekilis(topsayisi,üstsinir):
  ucret=0
  for x in range(topsayisi):
   numara = (random.randint(1, üstsinir))
   rakamlar.append(numara)
   ucret +=kolonfiyati
  return ucret

#top cekilis fonksiyonu
def topcekilis(topsayisi,üstsinir):
   olasilik=1
   for x in range(topsayisi):
    olasilik = olasilik *(1/üstsinir)
    üstsinir=üstsinir-1
   return (olasilik)

#beklenen değer
def ExpValue(ucret,olasilik,bikramiye):
    print("kazancın ortalaması")
    print(ucret*olasilik*bikramiye  )
    print("\n")

#biletin tutup tutmadığını gösteren fonksiyon
def biletkontrol(rakamlar,kullanicirakam):
  if(rakamlar==kullanicirakam):
     print("kazandiniz")
  else :
    print("kazanamadınız")

#ana fonksiyon
def main():
  ucret = cekilis(topsayisi,üstsinir)
  olasilik= topcekilis(topsayisi,üstsinir)
  ExpValue(ucret,olasilik,bikramiye)
  biletkontrol(rakamlar,kullanicirakam)

main()

import random

#cekilen top sayisi

topsayisi=7

#1 den n e kadar sayı üstsinir=n

üstsinir=90

#her kolon icin alınan ücret

kolonfiyati=3

#büyük ikramiye miktarları

bikramiye=5000000

#kullanıcının bileti

kullanicirakam=[1,2,3,4,1,2,2]

#kazanan bilet numaraların olduğu liste

rakamlar = []

#piyangoyu kazanan biletin ve bilet fiyatını bulan fonksiyonu

def cekilis(topsayisi,üstsinir):

ucret=0

for x in range(topsayisi):

numara = (random.randint(1, üstsinir))

rakamlar.append(numara)

ucret +=kolonfiyati

return ucret

#top cekilis fonksiyonu

def topcekilis(topsayisi,üstsinir):

olasilik=1

for x in range(topsayisi):

olasilik = olasilik *(1/üstsinir)

üstsinir=üstsinir-1

return (olasilik)

#beklenen değer

def ExpValue(ucret,olasilik,bikramiye):

print("kazancın ortalaması")

print(ucret*olasilik*bikramiye )

print("\n")

#biletin tutup tutmadığını gösteren fonksiyon

def biletkontrol(rakamlar,kullanicirakam):

if(rakamlar==kullanicirakam):

print("kazandiniz")

else :

print("kazanamadınız")

#ana fonksiyon

def main():

ucret = cekilis(topsayisi,üstsinir)

olasilik= topcekilis(topsayisi,üstsinir)

ExpValue(ucret,olasilik,bikramiye)

biletkontrol(rakamlar,kullanicirakam)

main()

yaptığımızda (görüldüğü üzere kazanamadık😀),beklenen değerimiz 0 a oldukça yakın çıktı.Kısacası eğlenmek için güzel fakat uzun vadede pek bir beklentide olmamamız daha iyi olur.Bu yazıdan sonra devam yazısında daha gerçekçi örneklerle karşınızda olucam.Okuduğunuz için teşekkürler ancak anlamadığınız ve/veya beğenmediğiniz şeyleri yazarak daha kaliteli içerikler üretilmesinde katkıda bulunabilirsiniz,herkese iyi çalışmalar |

KAYNAKÇA

Ders notlarım(Prof.Dr. İlhan USTA’nın derslerinden)
Nikos efthias (eski patronum)
Başıma yıldırım düştü-jeffrey S.Rosenthal
olasılık ve istatistik -prof.dr.fikri akdeniz
https://evrimagaci.org/kaos-teorisi-nedir-dogadaki-kaostan-soz-ederken-neyi-kastediyoruz-8198